Tutoriel
Ajouter une courbe de tendance à un graphique
Souvent nous nous servons d’un graphique pour mettre en forme des données, mais pour pouvoir les analyser il nous reste à les modéliser. Pour cela nous avons besoin de déterminer la courbe de tenance passant par chacun de nos points.
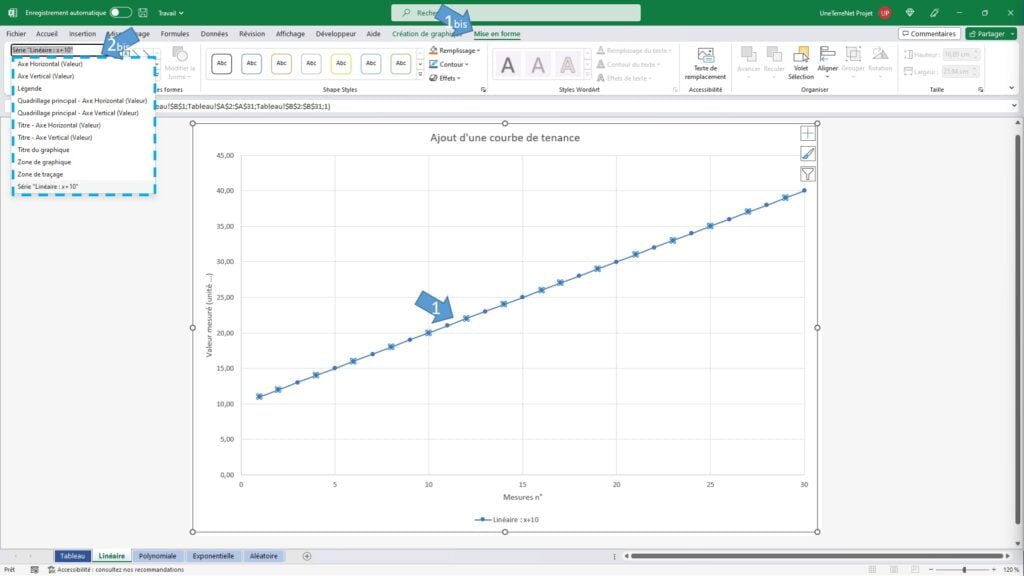
- Sélectionner une courbe dans votre graphique. Vous devez voir des petits carrés sur les points de la courbe sélectionné.
- Vous pouvez aussi aller dans l’onglet « Mise en forme » et sélectionnez votre courbe dans la liste déroulante à gauche.
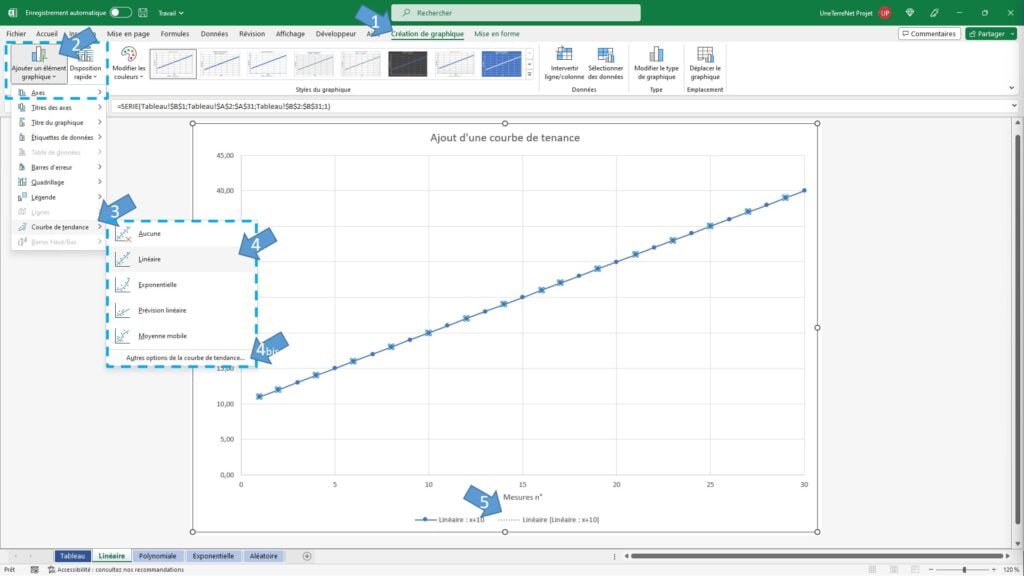
- Allez dans l’onglet « Création de graphique » puis dans la section « Disposition du graphique » et enfin cliquer sur « Ajouter un élément graphique ».
- Descendez dans courbes de tendances et cliquez sur le type de courbes que vous avez. Vous pouvez aussi cliquez sur « Autres options de la courbe de tendances… » pour ouvrir le bandeau de droite.
- Vous pouvez relever qu’un élément c’est ajouté dans la légende du graphique.
- Une autre solution est de faire un clic droit sur la courbe puis de sélectionner « Ajouter une courbe de tendance ». Je préfère cette méthode car elle ouvre directement le bandeau de droite.
- Si le bandeau de droite n’est pas affiché, faite un double clic sur la courbe de tendance. Il est possible que cette dernière ne soit pas très visible car superposé à la courbe de données, dans ce cas faites un double clic sur la courbe.

Afficher l’équation de la courbe de tendance
Maintenant qu’Excel à déterminer la courbe l’équation de la courbe il nous reste à déterminer son équation. Celle-ci permet de savoir pour chaque point de l’axe X le résultat sur l’axe Y, même les points n’étant pas compris dans notre tableau.
- Ouvrez le bandeau de droite si celui-ci n’est pas déjà ouvert. Faite un double clic sur la courbe de tenance et allez dans l’onglet option de la courbe de tenance.
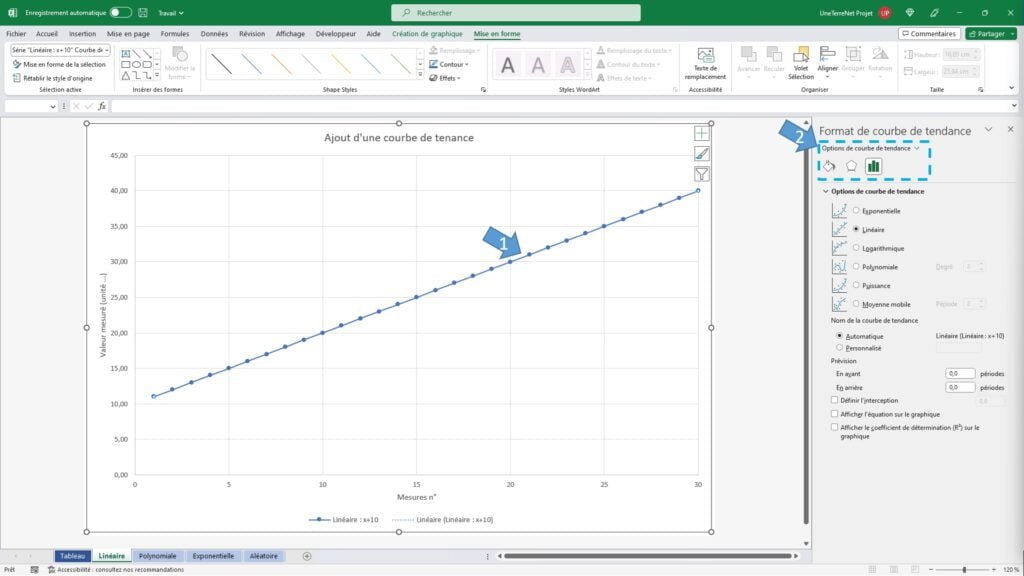
- En bas cliquez sur « Afficher l’équation sur le graphique ». L’équation va apparaitre sur le graphique.

- Notez qu’il est possible de projeter la courbe de tendance avant et après les points issus du tableau.
- Pour cela entrez des valeurs « En avant » et « En arrière » dans la zone de prévision. Le graphique est automatiquement mis à jour.

Afficher le coefficient de détermination R²
En plus de l’équation, Excel est capable de calculer le coefficient de détermination appelé R². Cette valeur permet de préciser à quel point la courbe est proche des données du tableau. Voyons cela avec un exemple :
- En bas du bandeau de droite cliquez sur « Afficher le coefficient de détermination (R²) sur le graphique ». Le coefficient va apparaitre sur le graphique juste en dessous de l’équation.

- Ici on voit que le coefficient est égal à 1. Cela s’explique car mes points ont été calculé avec l’équation, la même que celle déterminé par la tendance.
- Si j’ajoute une part variable aux points (je les décale de la courbes), on peut voir que l’équation et le coefficient évolue.

- Notez que si vous savez votre point au niveau de l’axe des ordonnées vous pouvez le spécifier.
- Cliquez sur « Définir l’interception » et entrée votre valeur. Dans mon cas c’est 10. Cela ajuste automatiquement mon équation et le coefficient.

Les différents types de tendances
Toute les courbes ne sont pas linéaires (des droites), c’est pour cela qu’Excel vous propose d’autres options de courbe de tendance.
- Si vous mettez une courbe de tendance linéaire sur cette courbe, celle-ci ne correspondra pas.
- Vous pouvez le constater visuellement et en regardant le coefficient de détermination.
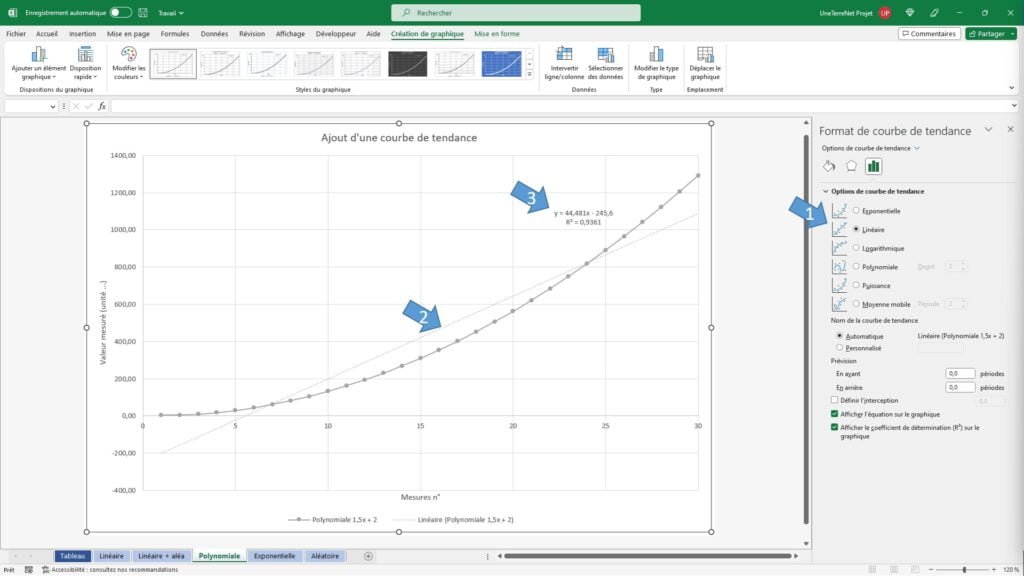
- Dans le bandeau de droite, textez de nouvelles options de courbes de tenances (Linéaire, exponentielle, logarithmique, polynomiale et puissance).
- Ici la solution est une polynomiale de degré 2.

- Et ici la solution est une exponentielle.

Les tendances de courbes aléatoires
Excel est un outil informatique bête et méchant, il fera toujours ce que vous lui demandez. Si vous lui dite d’exterminer l’humanité, heureusement il ne le fera pas car il ne comprendra pas mais si vous lui demandez de faire une courbe de tendance sur des valeurs aléatoire, il le fera.
- Prenons cette courbe générez avec une règle aléatoire, chaque point égal le point précédent plus une valeur aléatoire positive ou négative.
- Si nous traçons la courbe de tendance, Excel nous sortira un résultat, même si le coefficient de détermination est mauvais.

- Si vous jouez sur les paramètres vous pouvez améliorer le coefficient mais l’équation deviendra de plus en plus complexe.

- Théoriquement une équation avec une infinité de paramètre trouvera un coefficient proche de 1. Cela ne veut pas dire que l’analyse est juste.
- Pour des données aléatoire, le mieux que l’on puisse faire est de généré une moyenne mobile. Cela va en fait pour chaque point calculé la moyenne des points alentours. C’est très utile pour limiter le « bruit » ou les erreurs de mesures.
- Vous remarquerez que vue que ce n’est plus une équation mathématique, Excel n’affiche plus l’équation et le coefficient.